파이토치 자연어처리(15) - 확률적 경사 하강법

기존의 일반 경사하강법 : 전체 데이터를 모두 사용하여 기울기를 구함

ex) 한 번 파라미터 업데이트를 해줄 때 N개의 샘플이 전체 데이터셋이라면 그 전체 데이터셋을 모두 모델에 통과시켜야 했음 

-> 매우 많은 시간 소비 

 

확률적 경사하강법(SGD)

1. 랜덤 샘플링한 k개의 샘플을 모델에 통과시켜 손실값을 계산하고, 미분 이후에 파라미터 업데이트를 수행함 

2. 비복원 추출을 수행함 

 

* 비복원 추출

한 번 학습에 활용된 모든 샘플들은 모든 샘플들이 학습에 활용될 떄까지 다시 학습에 활용되지 않음 

 

*미니배치

랜덤 샘플링된 k개의 샘플들의 묶음 

미니배치의 크기가 작아질수록파라미터 업데이트 횟수가 늘어나게 된다. 

특별한 경우를 제외하고 256, 512의 크기를 가지는 것이 적당하다. 

 

확률적 경사하강법(SGD)의 파라미터 업데이트 동작 방식 

 

1. 

2. 

 

빨간색 : 앞에서 1번 째 샘플링되어 파라미터 업데이트할 때 사용했기 때문에 이번 2번 샘플링과정에 참여하지 않음 

노란색 : 이번 2번째 파라미터 업데이트에 사용될 샘플들 

 

즉, 기존 모델을 통과한 샘플들이 남지 않을 때까지 비복원 랜덤 추출이 되며, 랜덤 추출이 수행되며 샘플들이 전부 소진되게 되면 전체 샘플들에 대한 비복원 추출 진행 

 

*에포크 (Epoch)

전체 데이터셋의 샘플들이 전부 모델을 통과하는 것을 한 번의 에포크라고 한다. 

 

*이터레이션 (Iteration)

한 개의 미니배치를 모델에 통과시키는 것

 

# 전체 데이터셋 크기 N, 이터레이션(파라미터 업데이트) 횟수, 에포크 횟수, 미니배치 크기 k의 관계

 

 

# 미니배치 크기에 따른 SGD

미니배치의 크기가 데이터셋의 크기와 가까움 : SGD를 통해 얻은 크레디언트 방향 = GD를 통해 얻은 그래디언트 방향 (거의 정확한 그레디언트 방향에 가까움)

 

미니배치의 크기가 1에 가까움 : 전체 데이터셋의 분포와의 편향이 심해질 수 있음 

 

적절한 미치 배치의 크기 : 256

 

 

 

SGD 적용하기

 

1. 라이브러리와 데이터셋 로딩 불러오기 

 

import pandas as pd
import seaborn as sns
importmatplotlib.pyplot as plt

from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_california_housing

california = fetch_california_housing()     # 데이터셋 객체에 저장
df = pd.DataFrame(california.data, columns=california.feature_names) #데이터를 테이블 형식으로 보여준다. 이때 columns 속성은 열값들, 즉, price, region 등의 속성들을 나타냄
df["Target"] = california.target  #featurename과 target을 레코드(칼럼)로 갖는 데이터 테이블을 만듦

print(california.DESCR) #california의 정보 추출
print(california.feature_names) # 데이터 컬럼에 들어갈속성들 확인

df.tail()

 

 

2. 데이터 분포를 파악하기 위한 페어플롯 그리기

 

sns.pairplot(df.sample(1000)) #데이터셋 1000개 추출하여 임의로 그리기
pt.show()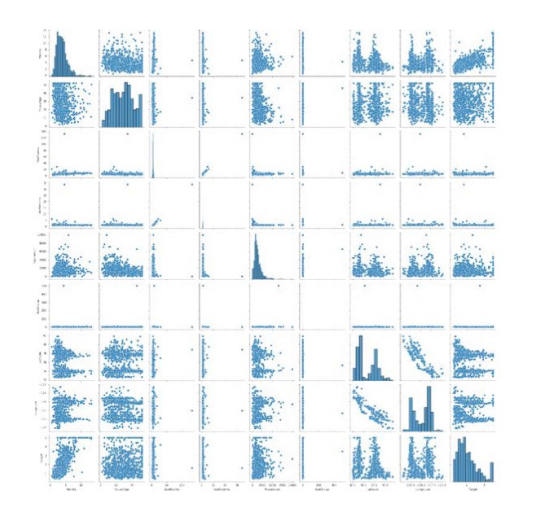

 

*멀티모달 분포 

2개 이상의 최빈값을 갖는 확률 분포

 

 

* 표준 스케일링

특성들의 평균을 0, 분산을 1 로 스케일링하는 것. 즉, 특성들을 정규분포로 만드는 것을 의미함

 

3. 위의 페어플롯에서 두 개 이상의 최빈값이 나오는 것드도 보이지만 일단 표준 스케일링을 해보자

 

scaler = StandardScaler()
scaler.fit(df.values[:,:-1])
df.values[:, :-1] = scaler.transform(df.values[:, :-1]) #스케일링을 위한 데이터 전처리 과정 fit -> transform

#df[행인덱스, 열인덱스] df[:,:-1] =df[전체 행 가져오기, ]
#df.values : 행들의 데이터들 가져오기
#df.values[:,:-1] : 전체 데이터 열의 마지막 칼럼(target=정답 칼럼)을 제외한 열들의 전체 데이터들 

#페어플롯 그리기
sns.pairplot(df.sample(1000)) # 정답칼럼을 뺀 데이터 전처리한 것들 pairplot으로 출력
plt.show()

 

4. 파이토치 모듈 불러오기 + 전처리된 데이터를 파이토치 텐서로 변환하고, x, y 지정해주기

 

#라이브러리 불러오기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

#앞에서 정제된 데이터를 파이토치 텐서로 변환하기
data = torch.from_numpy(df.values).float()

#파이토치 텐서 크기 확인하기
print(data.shape)

x = data[:, :-1] # 처음부터 target 컬럼을 제외한 나머지 컬럼들이 입력 데이터가 됨
y = data[:, -1:] # 맨 마지막 칼럼인target 컬럼(정답 컬럼)이 출력 데이터가 됨

print(x.shape, y.shape)

 

5. 학습에 필요한 세팅 값 지정 

 

n_epochs = 4000 #파라미터 업데이트 횟수
batch_size = 256 #배치 사이즈
print_interval = 200 #값 출력 2초간격
learning_rate = 1e -2 #학습률. 경사하강법에서 기울기에 학습률 곱해준다!

 

6. nn.Sequential 클래스로 심층 신경망을 구성하기 

model = nn.Sequential(
        nn.Linear(x.size(-1), 6),
        nn.LeakyReLU(),
        nn.Linear(6,5),
        nn.LeakyReLU(),
        nn.Linear(5,4),
        nn.LeakyReLU(),
        nn.Linear(4,3),
        nn.LeakyReLU(),
        nn.Linear(3, y.size(-1)),
        )
        
        # 첫 번째 선형 계층과 마지막 선형 계층은 실제 데이터셋 
        
print(model)
        


)

 

 

7. 파라미터를 학습시킬 옵티마이저 생성(확률적 경사하강법 옵티마이저)

 

optimizer = optim.SGD(model.parameters(), lr = learning_rate)

 

 

8.

 

바깥쪽 for 반복문 :

정해진 최대 에포크 수만큼 반복 수행하기 =  정해진 최대 에포크 수만큼 반복 수행하기(모델이 데이터셋을 n_epochs 만큼 반복해서 학습할 수 있도록 함 )

 

안쪽 for 반복문 : 

매 에포크마다 데이터셋을 랜덤하게 섞어 주고 미니배치로 나누게 된다. 

입력텐서 x와 출력텐서 y를 각각 따로 섞는게 아니라 함께 동일하게 섞어주어야 함!

 

 

#|x| = (total_size, input_dim)
#|y| = (total_size, output_dim)

#최대 에포크 수행하기 
for i in range(n_epochs):
    #Shuffle the index to feed-forward 
    #미니배치에 대해서 피드포워딩과 역전파, 경사하강을 수행함 
    
    #1. 셔플링하기  
    indices = torch.randperm(x.size(0))
    #torch.randperm() : 입력 데이터셋의 데이터들의 인덱스를 임의의 순서로 섞어준다. 
    x = torch.index_select(x, dim=0, index=indices)
    y = torch.index_select(y, dim=0, index=indices)
    #torch.index_select(데이터셋, 차원설정, index=순서) : 임의의 순서로 섞인 인덱스 순서대로 데이터를 배치한다. 
    
    #split : 원하는 배치 사이즈로 텐서를 나누어 미니배치를 만들기를 완료한다.
    x_ = x_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)
    # |x_[i]| = (batch_size, input_dim)
    # |y_[i]| = (batch_size, output_dim)
    
    #y_hat : 빈리스트 만들기
    y_hat = []
    #손실율 초기화
    total_loss = 0
    
    for x_i, y_i in zip(x_,y_):
        # 2. 미니배치 데이터를 모델에 학습시키기
        #|x_i| = |x_[i]|
        #|y_i| = |y_[i]|
        
        #미니배치마다 y_hat_i 변수에 피드포워딩 결과가 나오면 y_hat에 차례대로 저장하기  
        #위에서 만든 심층신경망 모델에 x를 넣어 y_hat에 차례대로 저장하기 
        y_hat_i = model(x_i)
        #F.mse_loss : 손실값 계산
        loss = F.mse_loss(y_hat_i, y_i)
        
        optimizer.zero_grad()
        loss.backward()
        
        optimizer.step()
        
        total_loss += float(loss)
        
        y_hat += [y_hat_i]
        
        total_loss = total_loss / len(x_)
        if (i+1) % print_interval == 0:
             print('Epoch %d : loss = %.4e' % (i+1, total_loss))
            
  y_hat = torch.cat(y_hat, dim=0)
  y = torch.cat(y_, dim=0)
  
  #|y_hat| = (total_size, output_dim)
  #|y| = (total_size, output_dim)

*optimizer.zero_grad()

 매번 loss.backward()를 호출할때 초기설정은 매번 gradient를 더해주는 것으로 설정되어있다.

그렇기 때문에 학습 loop를 돌때 이상적으로 학습이 이루어지기 위해선 한번의 학습이 완료되어지면(즉, Iteration이 한번 끝나면) gradients를 항상 0으로 만들어 주어야 함

S

*loss.backward()

 

 

 

9. 페어플롯으로 결과 확인하기 

 

df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach().numpy(),
            columns=["y", "y_hat"])
            #df라는 y와 y_hat을 칼럼으로 두고, y와 y_hat특성들의 관계도이고 이 관계는 2차원으로 추출한다. 
            #.detach() : 
            #.numpy() : 
sns.pairplot(df, height = 5) #y축 최대값을 5로 잡기
plt.show()